The concept of a situation extends the common notion of abstract object state[43,7]. Situations describe partial views of possible system-wide states, factored with respect to possibly several roles. In PSL, situations are represented by parameterized declarative expressions describing ``interesting'' commonalities of transient possible worlds in terms of relevant attribute and event predicate values. In PSL/IDL, a situation is represented as a parameterized predicate. We provide a full notation in [39], but use here an abbreviated form in which situations are defined within rules declarations as boolean C++ expressions within braces. (PSL/IDL-G notation is the same except that situations are demarcated by solid rounded boxes inside a dashed rules box.) Expressions may reference attributes and event predicates, named arguments and in-line local declarations. For example, the following situation describes the state of a File being open:
rules f1(File f) { { isOpen(f) } };
Realizations.
In the same sense that a class is instantiated by an object, and an
interface is instantiated by a role, a situation is said to be
instantiated by a realization. And just as interfaces describe
the properties of an unbounded family of potential implementations,
situations describe the properties of an unbounded family of potential
realizations. However, realizations are not explicitly
instantiated by programmers. They just unfold over the course of
system execution. For example, the realizations of the above
isOpen situation include all ``snapshots'' of a system in which such
a File is open. The manner in which such realizations are
observed or inferred in executing systems is outside the scope of PSL
proper (see Section 11).
A realization is thus a partial description of an arbitrarily brief
instance, an actual world in which the predicate describing a
situation holds. Realizations represent individual observations,
mappings, or inferences about concrete system behavior, characterized
by expressions describing attribute and event predicate values. A
realization is said to match one or more situations if all
features required in the situation(s) are present. The matching
relation, s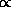 
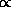S for realization s and
situation S, holds if the situation predicate for S can be
made true using the values in s (see [39]). Two or more
realizations may all match the same situation but in different ways
because they differently instantiate free parameters listed in the
situation.