


Next: Constraints
Up: Interface-Based Protocol Specification of
Previous: Situations
PSL temporal operators describe conditions under which realizations
occur. They are defined in terms of an underlying temporal dependency
relation a 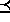 b among two realizations
a and b. If a
b among two realizations
a and b. If a 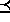 b, then a happens no
later than b (see Section 11). But since it
would not be very productive to describe protocols via orderings among
individual occurrences, PSL protocol rules are instead described at
the level of situations (classes of realizations). Each of the
following operators relates the occurrences of realizations of a
predecessor situation A and successor situation B:
b, then a happens no
later than b (see Section 11). But since it
would not be very productive to describe protocols via orderings among
individual occurrences, PSL protocol rules are instead described at
the level of situations (classes of realizations). Each of the
following operators relates the occurrences of realizations of a
predecessor situation A and successor situation B:
As lead to Bs: A 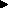 B
B 
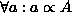

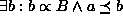
As enable Bs: A  B
B 
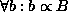

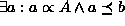
As pair with Bs: A  B
B 
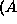
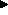
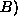
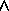
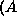

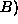
Rules are collections of situations linked by temporal operators. In
PSL/IDL-G, rules are expressed via lines connecting situations through
corresponding symbols drawn on the outside of the predecessor
situation to the same symbol drawn on the inside of the successor
situation. In PSL/IDL, these operators are designated as lead,
enable and pair respectively. In PSL/IDL (but not necessarily
in PSL/IDL-G), the ``earlier'' situation is always to the left of the
``later'' one. PSL/IDL situations are implicitly parameterized by the
arguments listed in their rules, as well as all declarations in
their predecessor situation(s).
Leading.
The ``forward reasoning'' operator A 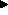 B is akin to a state
transition, applying to cases in which As always precede Bs.
However, unlike a state transition, A
B is akin to a state
transition, applying to cases in which As always precede Bs.
However, unlike a state transition, A 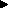 B does not indicate
that instances of B form the ``next'' situations after those of
A. Instead, an instance occurs at some unspecified time after an
instance of A occurs, in a manner that neither requires nor
precludes concurrency with respect to any other non-conflicting
rules. Also, unlike state transitions, the orderings are not
explicitly ``triggered'' by events. Instead predicates on events are
listed as aspects of the situations themselves. For example, a
protocol rule for a relay operation that sends m2 whenever
m1 is received takes the form (in PSL/IDL and PSL/IDL-G respectively):
B does not indicate
that instances of B form the ``next'' situations after those of
A. Instead, an instance occurs at some unspecified time after an
instance of A occurs, in a manner that neither requires nor
precludes concurrency with respect to any other non-conflicting
rules. Also, unlike state transitions, the orderings are not
explicitly ``triggered'' by events. Instead predicates on events are
listed as aspects of the situations themselves. For example, a
protocol rule for a relay operation that sends m2 whenever
m1 is received takes the form (in PSL/IDL and PSL/IDL-G respectively):
{in(m1)} lead {out(m2)}

This rule does not in any way imply that Relay operations must
be single-threaded. Because there are no constraints indicating
otherwise, two or more different ``threads'' of this rule may be
active concurrently, each triggered by a realization corresponding to
a different instance of an m1 message. On the other hand, this
specification does not preclude implementation via a single-threaded
relay object either.
Enabling.
The ``backward reasoning'' operator A  B is used for
relations in which A enables B, applying to cases in which
Bs are always preceded by As. (Or are ``caused'' by As, under
some interpretations of this overloaded term.) For example, a
desirable rule in most systems is the no spurious replies rule;
for any procedural message req:
B is used for
relations in which A enables B, applying to cases in which
Bs are always preceded by As. (Or are ``caused'' by As, under
some interpretations of this overloaded term.) For example, a
desirable rule in most systems is the no spurious replies rule;
for any procedural message req:
{in(req)} enable {out(reply[req]())}
This rule says that replies are sent only if messages are
received. It does not say that requests always lead to replies, only
that replies are never sent unless preceded by requests. In PSL/IDL,
this rule is considered to be predefined for all procedural requests,
since it is enforced by CORBA.
Separate rules may link multiple right-hand-sides to the same
left-hand-side to describe multiple possible effects. For example, we
could add another rule stating that req may lead to an
exception, and link it to the first rule, reflecting the fact that
rules are combined conjunctively (i.e., implicitly
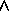 'ed):
'ed):
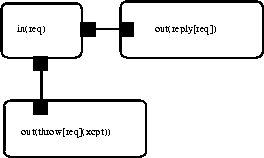
Pairing.
The A  B operator is used for if-and-only-if relations,
in which both every A is followed by a B, and every B is
preceded by an A; thus As and Bs occur only in pairs. For
example, another desirable global rule is the one-to-one delivery
rule, for any m:
B operator is used for if-and-only-if relations,
in which both every A is followed by a B, and every B is
preceded by an A; thus As and Bs occur only in pairs. For
example, another desirable global rule is the one-to-one delivery
rule, for any m:
{out(m)} pair {in(m)}

This says that all and only those messages that
have been issued are ultimately received. The  relation may
be used to provide guarantees about procedural operations. For
example, we could strengthen the above
relation may
be used to provide guarantees about procedural operations. For
example, we could strengthen the above  form to assert that a
reply to req must be issued, thus precluding the possibility of
exceptions or other non-procedural behavior:
form to assert that a
reply to req must be issued, thus precluding the possibility of
exceptions or other non-procedural behavior:
{in(req)} pair {out(reply[req]())}
Sequences. A single rule may include chains of
situations connected by temporal operators to describe sequencing. We
express sequences of, for example, the leads-to operator as A
 B
B  C. This indicates ( A
C. This indicates ( A  B)
B) 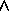 ( B
( B 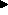 C) while also extending
scoping so that expressions in C may reference terms in A.
For example, a special protocol in which a relay outputs m3
after receiving message m1 followed by m2 could include a
rule of the form:
C) while also extending
scoping so that expressions in C may reference terms in A.
For example, a special protocol in which a relay outputs m3
after receiving message m1 followed by m2 could include a
rule of the form:
{in(m1)} lead {in(m2)} lead {out(m3)}
If we did not care about the ordering of m1 and m2, we
would have written this using simple conjunction of event predicates:
{in(m1), in(m2)} lead {out(m3)}
On the other hand, if we wanted to claim that this m1-m2 ordering
were the only one possible, we would add the rule:
{in(m1)} enable {in(m2)}



Next: Constraints
Up: Interface-Based Protocol Specification of
Previous: Situations
Doug Lea@Fri Mar 17 08:19:23 EST 1995
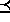 b among two realizations
a and b. If a
b among two realizations
a and b. If a 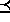 b, then a happens no
later than b (see Section 11). But since it
would not be very productive to describe protocols via orderings among
individual occurrences, PSL protocol rules are instead described at
the level of situations (classes of realizations). Each of the
following operators relates the occurrences of realizations of a
predecessor situation A and successor situation B:
b, then a happens no
later than b (see Section 11). But since it
would not be very productive to describe protocols via orderings among
individual occurrences, PSL protocol rules are instead described at
the level of situations (classes of realizations). Each of the
following operators relates the occurrences of realizations of a
predecessor situation A and successor situation B: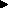 B
B 
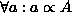

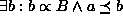
 B
B 
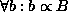

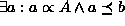
 B
B 
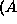
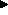
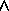
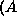

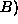
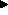 B is akin to a state
transition, applying to cases in which As always precede Bs.
However, unlike a state transition, A
B is akin to a state
transition, applying to cases in which As always precede Bs.
However, unlike a state transition, A 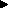 B does not indicate
that instances of B form the ``next'' situations after those of
A. Instead, an instance occurs at some unspecified time after an
instance of A occurs, in a manner that neither requires nor
precludes concurrency with respect to any other non-conflicting
rules. Also, unlike state transitions, the orderings are not
explicitly ``triggered'' by events. Instead predicates on events are
listed as aspects of the situations themselves. For example, a
protocol rule for a relay operation that sends m2 whenever
m1 is received takes the form (in PSL/IDL and PSL/IDL-G respectively):
B does not indicate
that instances of B form the ``next'' situations after those of
A. Instead, an instance occurs at some unspecified time after an
instance of A occurs, in a manner that neither requires nor
precludes concurrency with respect to any other non-conflicting
rules. Also, unlike state transitions, the orderings are not
explicitly ``triggered'' by events. Instead predicates on events are
listed as aspects of the situations themselves. For example, a
protocol rule for a relay operation that sends m2 whenever
m1 is received takes the form (in PSL/IDL and PSL/IDL-G respectively):

 B is used for
relations in which A enables B, applying to cases in which
Bs are always preceded by As. (Or are ``caused'' by As, under
some interpretations of this overloaded term.) For example, a
desirable rule in most systems is the no spurious replies rule;
for any procedural message req:
B is used for
relations in which A enables B, applying to cases in which
Bs are always preceded by As. (Or are ``caused'' by As, under
some interpretations of this overloaded term.) For example, a
desirable rule in most systems is the no spurious replies rule;
for any procedural message req:
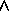 'ed):
'ed):
 B operator is used for if-and-only-if relations,
in which both every A is followed by a B, and every B is
preceded by an A; thus As and Bs occur only in pairs. For
example, another desirable global rule is the one-to-one delivery
rule, for any m:
B operator is used for if-and-only-if relations,
in which both every A is followed by a B, and every B is
preceded by an A; thus As and Bs occur only in pairs. For
example, another desirable global rule is the one-to-one delivery
rule, for any m:

 relation may
be used to provide guarantees about procedural operations. For
example, we could strengthen the above
relation may
be used to provide guarantees about procedural operations. For
example, we could strengthen the above  form to assert that a
reply to req must be issued, thus precluding the possibility of
exceptions or other non-procedural behavior:
form to assert that a
reply to req must be issued, thus precluding the possibility of
exceptions or other non-procedural behavior:
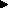 B
B 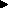 C. This indicates ( A
C. This indicates ( A 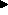 B)
B) 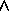 ( B
( B 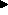 C) while also extending
scoping so that expressions in C may reference terms in A.
For example, a special protocol in which a relay outputs m3
after receiving message m1 followed by m2 could include a
rule of the form:
C) while also extending
scoping so that expressions in C may reference terms in A.
For example, a special protocol in which a relay outputs m3
after receiving message m1 followed by m2 could include a
rule of the form: