


Next: Examples
Up: PSL: Protocols and Pragmatics
Previous: Specification
As a basis for specification, PSL relies on any framework for
declaring interface types that minimally include operation signatures
in their declarations, and where signatures are based on any
reasonable type system on pure value types such as integers, booleans,
reals, records, etc. PSL specifications provide additional constraints
and rules that hold for all role instances of the associated
interfaces.
To extend interface-based specification we introduce three
notations. Our primary PSL notation helps define basic abstractions.
However, rather than establishing a general syntax for expressions,
types, interfaces, and so on, we illustrate using PSL/IDL, a concrete
syntax for PSL using CORBA IDL value and interface types and
C/C++-style expressions, geared for use in CORBA systems. Also,
because representations of even simple protocols stretch the limits of
readability and writability in textual form, we simultaneously define
PSL/IDL-G ProtocolCharts, a semigraphical form of PSL/IDL
corresponding in simple ways to the textual representation.
PSL/IDL role types are synonymous with CORBA IDL interfaces. All
PSL/IDL constructs appear as annotations within protocol
module declarations that have the syntactic properties of IDL
modules but contain only type declarations, attribute function
declarations, and/or rules declarations. A PSL/IDL rules
declaration is an optionally named scope, parameterized over one or
more types, and containing protocol rules and/or constraint rules.
PSL/IDL uses C/C++ expression syntax over CORBA IDL value types.
Predicates are boolean expressions. For convenience, we add the
logical implies operator (`` -->'') and its left-sided
version, is implied by (`` <--'') to the list of boolean
operators. Within expressions, commas may be used as low-precedence
and separators (otherwise equivalent to &&). The fields
of IDL exception, struct and union values are
referenced using dot notation. To make them more useful in
specifications, PSL/IDL predefines common pure value functions on the
IDL sequence and string types. The functions head,
tail, empty, contains, prepend, append,
concat, equal and remove are predefined for
sequences of all types for which there exists an equality operation.
Definitions are identical to those on parameterized list types in
functional programming languages such as ML [69]. PSL/IDL does not
define types for sets, multisets, or maps. Sequence types may be used
to equivalent effect.
For purposes of specification, each distinct instance of a role is
ascribed a unique handle. Handles are an abstraction of
names [48], references [52], ports [65], static
labels, etc., used to identify role instances and message
destinations. Handles are not references to objects, nor
are they implementation-level pointers to concrete components,
although there may be a one-to-one relationship between handles and
pointers in a particular mapping to a programming language, tool, or
infrastructure.
PSL relies on the existence of one or more handle types, and handle
values that may be used in any value context. There may be several
distinct handle types in a system. Handle types may include values
that do not provide access to implementations (as in the case of
``null'' and ``dangling'' references), in which case we say that the
handle is not live. The equality relation `` =='' among
handle values denotes only value equality among handles (also known as
``shallow'' equality), not necessarily identity or equality of
implementation-level components.
PSL/IDL handle values are expressed using the syntax of IDL
objrefs. These serve as both references to instances of IDL
interfaces ( not necessarily their implementations) and
destinations of CORBA messages. However, as discussed in Section
3.4 and the Appendix, PSL handle values need not bear a
one-to-one relation with objref values in CORBA implementations.
An attribute (also known as a state function[39,34]) is
an abstract property ascribed to zero or more role instances, and
possibly assuming different values across time. In PSL, attributes
are abstract functions of handle and/or other value type arguments;
for example function isOpen takes a File handle as an
argument.
As with other PSL constructs, the relationship between abstract
attributes and their implementations (if any) is outside the scope of
the framework. For example, the attribute isOpen is a
hypothetical function that might actually be computed (perhaps only
approximately; see Section 5) as a
side-effect-free procedure, a function whose value is deduced by an
analytic tool, and/or a ``derived'' function that is symbolically
definable or otherwise constrained in terms of other attributes. The use of an
attribute in PSL does not commit implementations to ``know'' its
values in any computational sense, and even if implemented, does not
mandate that the value be computed by any component it describes.
In PSL/IDL, attributes are declared as auxiliary functions within the
scope of a protocol module using normal IDL/C++ function syntax,
and where all function arguments are explicit. For example:
interface File { /* ... */ };
protocol module fm {
boolean isOpen(File f);
};
PSL/IDL uses function syntax rather than IDL
attribute syntax. In IDL, the keyword attribute is only a
stylistic device for declaring accessor and mutator operations
within interfaces. There is no PSL/IDL-G notation for declaring
attributes, although OMT [61] or related object-oriented
graphical notations can be used (see Section 4.4).
Among the most common forms of attributes used in PSL are
``relational'' or ``connection'' attributes that represent the values
of handles that a participant uses to communicate with others. For
example, a File might be ascribed attribute IODevice
Dev(File f) representing a handle used in I/O requests. As is true
for any attribute, the values of connection attributes may vary over
time, subject to any other listed constraints.
The concept of a situation extends the common notion of abstract
object state [44,7]. Situations describe
partial views of possible system-wide states, factored with respect
to particular roles. Thus, a situation may describe the abstract
state of multiple components. Situations are defined declaratively, at
any level of granularity. In PSL, situations are represented by
parameterized expressions describing ``interesting'' commonalities of
transient ``possible worlds''. These expressions classify aspects of
worlds in terms of characteristic values of relevant attributes and
event predicates with respect to one or more roles.
In the same sense that a class is instantiated by an object, and an
interface is instantiated by a role, a situation is said to be
instantiated by a realization. And just as interfaces describe
the properties of an unbounded family of potential implementations,
situations describe the properties of an unbounded family of potential
realizations. However, realizations are not explicitly
instantiated by programmers. They just unfold over the course of
system execution. For example, a situation might contain only the
constraint that a given kind of File is open. The realizations of this
situation in a particular system include all ``snapshots'' of the
system in which such a File is open. The manner in which such
realizations are observed or inferred in executing systems is outside
the scope of PSL proper (see Section 5).
A realization is thus a partial description of an arbitrarily brief
instance, an ``actual world'', in which the predicate describing a
situation holds. Realizations represent individual observations,
mappings, or inferences about concrete system behavior, characterized
by expressions describing attribute and event predicate values.
A realization is said to match one or more situations if all
features required in the situation(s) are present. The matching
relation, r 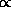 S for realization r and
situation S, holds if the situation predicate for S can be
made true using the values in r (see Appendix). Two or more
realizations may all match the same situation but in different ways
because they differently instantiate free parameters listed in the
situation.
S for realization r and
situation S, holds if the situation predicate for S can be
made true using the values in r (see Appendix). Two or more
realizations may all match the same situation but in different ways
because they differently instantiate free parameters listed in the
situation.
A situation is represented as a parameterized predicate. We provide a
full notation in the Appendix, but use here an abbreviated form in
which situations are defined within rules declarations as
boolean C/C++-style expressions within braces. Expressions inside
situations may reference attributes and event predicates, and may
include references to named arguments. They may also include in-line
local declarations (which have the expression value of true).
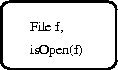
For example, assuming the definition of an isOpen attribute the
following situation describes the state of a File being open:
rules f1(File f) {
{ isOpen(f) }
};
PSL/IDL-G notation is the same except that situation
expressions are demarcated by solid rounded boxes. They may be
embedded within a rules declaration drawn with a dashed box with
name and parameters in the corner. However, in PSL/IDL-G, it is
usually more convenient to use ``in-line'' declarations in situation
boxes rather than explicit rules parameterization:
Messages carry communications among participants, including operation
requests, operation replies, asynchronous messages, exceptions, and so
on. For each kind of message M possible in a system, PSL
assumes the existence of a corresponding record type
MessageType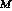 that minimally includes fields describing the message
``selector'' (e.g., operation name) and arguments (if any). We will
illustrate PSL usage in systems of fixed message types. However, at an
extreme, all messages in a system might have the same selector, with
an argument format requiring dynamic interpretation. Message types
may vary over any number of dimensions. For example, all messages of
a certain type may include fields suitable for use in routing over a
particular topology of distributed components.
that minimally includes fields describing the message
``selector'' (e.g., operation name) and arguments (if any). We will
illustrate PSL usage in systems of fixed message types. However, at an
extreme, all messages in a system might have the same selector, with
an argument format requiring dynamic interpretation. Message types
may vary over any number of dimensions. For example, all messages of
a certain type may include fields suitable for use in routing over a
particular topology of distributed components.
Messages are assumed in PSL to be handle-directed. A handle
describing the intended receiver role is a required part of any
communication. Similarly, messages corresponding to a procedural
operation that returns a reply (or perhaps just a `` void''
completion indication) include a handle describing the ``return
address'' of the caller. We also assume an abstract function
reply[ msg] that represents a reply message (not its issuance) of
the appropriate type for a given procedural request msg, and a
function throw[ msg] that represents an exception reply message
for a request. As a notational convenience, a reply or
throw without a bracketed message argument refers to the most closely
associated message whenever this is unambiguous.
PSL/IDL message types are abstractions of CORBA::Request, with a
shorthand handle-based message syntax delimited by angle-brackets:
m = < dest-> op( args) >
Here, m is an instance of an implicitly ``pattern-matched'' message
type corresponding to the form of the message expression; dest is a
handle indicating the destination role instance of the message; op
is an operation name literal; and args are arguments, each of some
value type as defined in a corresponding interface. Messages need not
be named, and values are referenced directly rather than through the
implicit fields of m. Bindings for arguments follow normal IDL
rules.
While PSL/IDL message conventions correspond closely to those used in
CORBA, the relation need not be one-to-one. Mappings between handles
and the values used in CORBA message destination fields may take
several forms, even within the same CORBA
implementation [56,27]. For example, channel-style
objrefs may be used. Channel values [65] represent
``paths'' to role instances. Two or more messages sent with the same
channel identifier reach the same instance, but two channel values
that access the same interface instance may differ. Object-reference
style objrefs may also be used so long as messages are always
delivered to implementation objects corresponding to the appropriate
roles; for example when references are routed through proxies that
relay messages to the appropriate implementations. Other syntactic
details and mappings to base PSL constructs may be found in the
Appendix.
Messages themselves are not used directly in PSL situation
descriptions. Instead, PSL contains two families of special attribute
functions, in and out. Inside situations, in(
m ) by( p ), where m is of some type
MessageType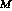 and p is a handle value, denotes a context in
which a particular message instance m has been received by
participant p, and out( m ) by( p )
denotes a context in which m has been issued by p. The
by( p ) suffixes are optional and seldom needed. When
otherwise unconstrained by context, omission reflects lack of
commitment about which participant issues or receives a message.
and p is a handle value, denotes a context in
which a particular message instance m has been received by
participant p, and out( m ) by( p )
denotes a context in which m has been issued by p. The
by( p ) suffixes are optional and seldom needed. When
otherwise unconstrained by context, omission reflects lack of
commitment about which participant issues or receives a message.
PSL event predicates are otherwise treated as attribute functions that
happen to have predefined characteristics. In particular, events never
``unhappen'': Once a predicate describing the occurrence of an
individual event becomes true, it never becomes false. Event
predicates are monotonic attributes, behaving as persistent
``latches''. Once out( m ) by( p ) is true
for a particular m and p, it is true forever more;
similarly for in( m ) by( p ). Situations
and rules may thus be phrased in terms of events that have occurred at
any time (cf., [45]).
PSL/IDL event predicates use PSL/IDL messages as arguments to in
and out. For example, assuming declarations of aFile,
c, and exc within the scope of a given rules declaration
or in referenced IDL interface declarations:
in( <aFile->write(c)> )
out( reply[<aFile->read()>](c) )
out( throw(exc) ) by(aFile)
PSL protocol rules describe conditions under which realizations of
situations occur. Rules are collections of situations linked by
temporal operators. These temporal operators are defined in terms of
an underlying temporal dependency relation a 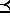 b
among two realizations a and a. If a
b
among two realizations a and a. If a 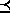 b, then a happens no later than a. (See Section
3.10 for a more formal characterization.) The means
by which this relation is observed or arranged lies outside of the
scope of PSL proper (see Section 5).
b, then a happens no later than a. (See Section
3.10 for a more formal characterization.) The means
by which this relation is observed or arranged lies outside of the
scope of PSL proper (see Section 5).
Since it would not be very productive to describe protocols via
orderings among individual occurrences, PSL protocol rules are instead
described at the level of situations (classes of realizations). Each
of the following operators relates the occurrences of realizations of
a predecessor situation A and successor situation B:

In PSL/IDL-G, rules are expressed via arrows connecting situations
through corresponding symbols drawn on the outside of the predecessor
situation. In PSL/IDL, these operators are designated as lead,
enable and pair respectively. In PSL/IDL (but not necessarily
in PSL/IDL-G), the ``earlier'' situation is always to the left of the
``later'' one.
The ``forward reasoning'' operator A  B is akin to that of
a state transition, applying to cases in which As always precede
Bs. However, unlike a state transition, A
B is akin to that of
a state transition, applying to cases in which As always precede
Bs. However, unlike a state transition, A  B does not
indicate that instances of B form the ``next'' situations after
those of A. Instead, an instance occurs at some unspecified time
after an instance of A occurs, in a manner that neither requires nor
precludes concurrency or interleavings with respect to any other
non-conflicting rules. Also, unlike state transitions, the orderings
are not explicitly ``triggered'' by events. Instead predicates on
events are considered to be aspects of the situations themselves.
B does not
indicate that instances of B form the ``next'' situations after
those of A. Instead, an instance occurs at some unspecified time
after an instance of A occurs, in a manner that neither requires nor
precludes concurrency or interleavings with respect to any other
non-conflicting rules. Also, unlike state transitions, the orderings
are not explicitly ``triggered'' by events. Instead predicates on
events are considered to be aspects of the situations themselves.
For example, a protocol rule for a relay operation that sends m2
whenever m1 is received takes the form:
{in(m1)} lead {out(m2)}

In the scope of a particular PSL/IDL protocol, we would have to be
more explicit about types and messages.
PSL/IDL rules always lie within the scope of a given rules
declaration. PSL/IDL situations are implicitly parameterized by the
arguments listed in their rules, as well as all declarations in
their predecessor situation(s). All rules parameters implicitly
serve as universal quantifiers for the enclosed expressions, and other
inline declarations are implicitly existentially quantified. The PSL
matching relation (``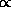 '') requires that unambiguous names be
used in any two situations related by operators. To ensure this, any
situation expression may reference, but not redeclare, any symbol
declared in its rules and its predecessors. Thus, all value
names in a set of ordered situations must be unique (see Appendix).
'') requires that unambiguous names be
used in any two situations related by operators. To ensure this, any
situation expression may reference, but not redeclare, any symbol
declared in its rules and its predecessors. Thus, all value
names in a set of ordered situations must be unique (see Appendix).
For example, a relay that accepts a (where a is a handle
of a role supporting operation m2) as an argument of m1
and then issues m2 to a:
rules r1(Relay r) {
{in(<r->m1(a)>)} lead {out(<a->m2()>)}
};

This rule does not in any way imply that Relay operations must
be single-threaded. Because there are no constraints that indicate
otherwise, two or more different ``threads'' of this rule may be
active concurrently, each triggered by a realization corresponding to
a different instance of an m1 message. On the other hand, this
specification does not preclude implementation via a single-threaded
relay object either.
Once a predicate describing the occurrence of an individual event
becomes true, it never becomes false. Thus, event predicates
``latch'' from left to right in PSL linked situations. For any event
predicate e, if e holds in A, then it also holds in
all successors of A. (This property does not necessarily
hold for expressions on attributes that are not tied to event
predicates). For example, the first relay rule is equivalent to one
explicitly mentioning in(m1) in the successor situation:
{in(m1)} lead {in(m1), out(m2)}
The ``backward reasoning'' operator A
 B is used for relations in which A enables
B, applying to cases in which Bs are always preceded by
As. (Or are ``caused'' by As, under some interpretations
of this overloaded term.) For example, a desirable rule in most
systems is the no spurious replies rule, saying that replies are
sent only if messages are received. It does not say that requests
always lead to replies, only that replies are never sent unless
preceded by requests. In PSL/IDL, this rule is considered to be
predefined for all procedural requests, since it is enforced by CORBA:
B is used for relations in which A enables
B, applying to cases in which Bs are always preceded by
As. (Or are ``caused'' by As, under some interpretations
of this overloaded term.) For example, a desirable rule in most
systems is the no spurious replies rule, saying that replies are
sent only if messages are received. It does not say that requests
always lead to replies, only that replies are never sent unless
preceded by requests. In PSL/IDL, this rule is considered to be
predefined for all procedural requests, since it is enforced by CORBA:
{in(req)} enable {out(reply[req]())}
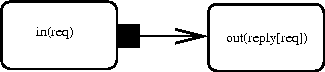
Separate rules may link multiple right-hand-sides to the same
left-hand-side to describe multiple possible effects. For example, we
could add another rule stating that req may lead to an
exception. This may be pictured together with the first rule,
reflecting the fact that rules are combined conjunctively (i.e.,
implicitly 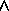 'ed):
'ed):
The A  B operator is used
for if-and-only-if relations, in which both every A is followed
by a B, and every B is preceded by an A; thus
As and Bs occur only in pairs. For example, another desirable
global rule is the one-to-one delivery rule, for any m,
saying that all and only those messages that have been issued are
ultimately received.
B operator is used
for if-and-only-if relations, in which both every A is followed
by a B, and every B is preceded by an A; thus
As and Bs occur only in pairs. For example, another desirable
global rule is the one-to-one delivery rule, for any m,
saying that all and only those messages that have been issued are
ultimately received.
{out(m)} pair {in(m)}

The  relation may be used to provide guarantees about
procedural operations. For example, we could strengthen the above
relation may be used to provide guarantees about
procedural operations. For example, we could strengthen the above
 form to assert that a reply to req must be issued,
thus precluding the possibility of exceptions or other non-procedural
behavior:
form to assert that a reply to req must be issued,
thus precluding the possibility of exceptions or other non-procedural
behavior:
{in(req)} pair {out(reply[req]())}

A single rule may include chains of situations connected by temporal
operators to describe sequencing. We express sequences of, for
example, the leads-to operator as A  B
B  C. This indicates (A
C. This indicates (A  B)
B) 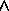 (B
(B
 C) while also extending scoping so that expressions in
C may reference terms in A. Chains across the other
operators are expressed similarly. For example, a special protocol in
which a relay outputs m3 after receiving the ordered fixed
messages m1 followed by m2 could include a rule of the
form:
C) while also extending scoping so that expressions in
C may reference terms in A. Chains across the other
operators are expressed similarly. For example, a special protocol in
which a relay outputs m3 after receiving the ordered fixed
messages m1 followed by m2 could include a rule of the
form:
{in(m1)} lead {in(m2)} lead {out(m3)}

If we did not care about the ordering of m1 and m2, we
would have written this using simple conjunction of event predicates:
{in(m1), in(m2)} lead {out(m3)}
On the other hand, if we wanted to claim that this m1-m2 ordering
were the only one possible, we could add the rule:
{in(m1)} enable {in(m2)}
Some conditions must always hold, across all possible contexts.
Constraint rules limit the set of possible system states to those in
which the expressions hold. For a trivial example, if we declared
attribute notOpen(File f), we would want to claim that its value
is always equal to !isOpen(f).
The PSL notation for static constraints is based on the
necessity operator of temporal and modal
logic [20,66], operator  . The expression
. The expression  P indicates that P invariantly holds for all time, over all
possible worlds. All realizations must obey
P indicates that P invariantly holds for all time, over all
possible worlds. All realizations must obey  constraints in
addition to those explicitly listed in situations. In PSL/IDL
rules declarations, brace-demarcated expressions describing necessary
restrictions among attribute values are prefaced by inv. In
PSL/IDL-G, they are listed with an unfilled box on their sides. For
example:
constraints in
addition to those explicitly listed in situations. In PSL/IDL
rules declarations, brace-demarcated expressions describing necessary
restrictions among attribute values are prefaced by inv. In
PSL/IDL-G, they are listed with an unfilled box on their sides. For
example:
rules f1(File f) {//...
inv {notOpen(f) == !isOpen(f)}
};

One common use of constraints is to relate non-monotonic time-varying
attributes to PSL ``latching'' event predicates. For example,
supposing that our unrealistically simple File may be opened and
closed only once, we might supply constraints indicating how attribute
isOpen varies with open and close events. Among
other possibilities, we could write this via the pair of implication
constraints:
rules f1(File f) { //...
inv {isOpen(f) --> out(reply[<f->open()>]()) }
inv {out(reply[<f->close()>]()) --> !isOpen(f) }
};
Here, the first constraint says that if a file is open, then it must
have at some time replied to an open request (but not
necessarily vice versa). The second says that if the file has ever
replied to a close request, then it must not be open. These
constraints might be buttressed with a description of a
FileFactory operation that guarantees that isOpen is true upon
reply of its File handle result.
While constraints are typically used to relate conceptual attributes
to event predicates in this manner, it is not at all required, and
sometimes not even possible to do so. For example, if a File
could be implemented by a special kind of object that is initially
open upon construction without requiring an explicit open
operation, then the first constraint above would not hold. More
generally, attributes associated with ``base'' interfaces are often
only weakly constrained. They are further constrained in declarations
associated with different subinterfaces. However, while convenient,
and sometimes unavoidable, the use of unconstrained attributes is also
notoriously troublesome in practice [44,12,19], and
requires care in specification. When attributes are not tied to
events, there are no global rules stating how values change as a
function of events. As illustrated in Section
4.5, any required variation or invariance in
the values of unconstrained attributes across time must be explicitly
tracked in individual protocol rules.
Constraint rules may also relate event predicates. PSL does not
notationally distinguish constraints that are ``definitionally'' true
versus those that are required to be true as a matter of system
policy. For example, to reflect the common requirement that either a
normal reply or an exceptional reply can be issued for request
req, but at most one of these, we could list:
inv {out(reply[req]()) --> !out(throw[req](x))}
inv {out(throw[req](x)) --> !out(reply[req]())}
inv {out(r1 = reply[req]()) && out(r2 = reply[req]()) --> (r1 == r2)}
inv {out(t1 = throw[req](x)) && out(t2 = throw[req](y)) --> (t1 == t2)}
Because CORBA (like most systems) enforces these conventions for all
procedural messages, such rules are predefined for all message and
exception types in PSL/IDL.
The third and fourth rules above employ a standard logic trick for
declaring uniqueness. The third rule says that if there are two values
matching reply[req]() then they must be the same message. This
kind of constraint is common enough that we define the PSL/IDL
``macro'' unique( expr ), which is false if there is
more than one match. For example, we could rephrase the last two rules
above as:
inv {unique(reply[req]())}
inv {unique(throw[req](x))}
Like interfaces, states and classes, situations may be specialized
into subsituations. Subsituation relations are analogs of the
subtype relations underlying interface inheritance. Mechanics follow
those for ordinary sets defined via predicates. For example, situation
Q: {in(readrequest) && isOpen(f)} is a subsituation of
P: {in(readrequest)} in which case we say that Q
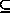 P.
P.
If Q 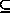 P, then fewer possible realizations match
Q than P. Every situation is a subsituation of the empty
situation
P, then fewer possible realizations match
Q than P. Every situation is a subsituation of the empty
situation {} (or equivalently {TRUE}), which is matched
by all realizations. The situation {FALSE} (matched by no
realizations) is a subsituation of all others. We say that expression
expr holds in situation S if S 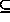
{ expr }. Conversely, we define set-like union and
intersection operators in terms of the corresponding boolean relations
on their component expressions [19,63]. In PSL/IDL A
 B is expressed as
B is expressed as { expr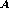
}
&& { expr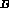
}, and A  B
as
B
as { expr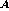
} || {
expr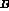
}.
The simplest and most common means of constructing a subsituation is
to ``strengthen'' an expression by and'ing an independent
predicate p, since A 
{ p}
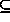 A. Strengthening may also occur by replacing a
predicate with one that implies it. For example, a situation
including out( m) might be strengthened by replacing it
with the more committal out( m)by( p ).
A. Strengthening may also occur by replacing a
predicate with one that implies it. For example, a situation
including out( m) might be strengthened by replacing it
with the more committal out( m)by( p ).
PSL does not use any special notation to declare that one
situation is a subsituation of another except in the special case of
disjoint union where S = S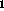 + S
+ S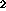 + ... + S
+ ... + S . This represents a set of
subsituations S
. This represents a set of
subsituations S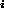 that are constrained to completely partition
a situation-space S. Partitioned subsituations must be
exhaustive and mutually exclusive. They cannot simultaneously
hold. Partitioning is thus one way to express the notion that one
situation ``disables'' another [70].
that are constrained to completely partition
a situation-space S. Partitioned subsituations must be
exhaustive and mutually exclusive. They cannot simultaneously
hold. Partitioning is thus one way to express the notion that one
situation ``disables'' another [70].
In PSL/IDL, partitions are enclosed in cases of the form {
case S
case S ...
... case
{default} }. Successive cases are interpreted in the
same way as case, cond, and if ... elsif
statements in most languages, implicitly negating the expressions in
all previous cases. The special trailing situation default
matches only if all previous cases fail, thus acting as a generalized
else. Properties common to all partitions may be expressed by
linking a situation with the common expressions to all partitions via
&& to the cases.
In PSL/IDL-G, partitioning is indicated via nested
stateCharts [25]. Each enclosed box represents a
partition. The special trailing ``else'' box contains only the
expression default. Expressions common to all partitioned
subsituations may be listed outside of the nested boxes.
Conditional protocol rules can be expressed using partitions.
Ordering operators ``distribute'' through situation partitionings to
describe conditional paths. For example, to indicate that a
TRUE reply is enabled if some function ok holds, and conversely
for FALSE:
{in(req)} && {
case {ok(req)} enable{out(reply(TRUE))}
case {default} enable{out(reply(FALSE))}
}

Protocol refinement is the act of introducing new rules that apply in
more specific situations than do general rules, without invalidating
these more general rules. Refinement constraints maintain consistency
among these related rules and contexts.
In PSL, refinements are normally localized to new entities described
by new interfaces bearing subinterface relations to the originals.
PSL protocol declarations are parameterized with reference to
interface types. Specialized protocol declarations may be attached to
(parameterized by) instances of subinterfaces. Attaching new rules to
subinterfaces allows commitment to more specific protocols in special
cases, without overcommitting in the general case. Similarly, placing
generalizations of existing rules in a supercontext supports simpler
high-level views and allows other alternative specializations.
In PSL/IDL, when two kinds of roles differ in protocol but not
operation signatures (for example, when protocols differ across
``local'' versus ``remote'' versions of components), this may require
construction of ``dummy'' IDL interface types just to give the two
types different names (cf., [5]).
Of course, not all reasonable modifications are valid refinements. For
example, instances of a protocol description could differ in that one
corrects an error, or removes unwanted behavior, or describes a subtly
different protocol, or imposes additional constraints due to changed
or overlooked requirements. Valid refinements are generally limited
to the following techniques, that may also be applied in reverse in
the course of generalization. These techniques reflect properties of
PSL that hold for all situations A, B, C containing
predicates meaningful in their scopes:

New rules relating new situations, as well as new constraints, may be
added so long as they do not conflict with existing ones. For
example, if ReadWriteFile is defined as a subinterface of
ReadFile, new rules applicable to write operations may be
defined in rules for ReadWriteFile. The rules for
ReadFile would also still hold for all ReadWriteFile
instances.
A new situation S may be spliced among existing ordered
situations A and B, so long as the original relation
between A and B is maintained. Thus, A  B may be extended to A
B may be extended to A  S
S  B,
or to A
B,
or to A  B
B  S, or to the separate
(A
S, or to the separate
(A  S)
S) 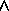 (A
(A  B), and so
on. Splicing allows arbitrarily complex subprotocols to be inserted
between specified end-points. For example, a coarse-grained
specification of a rule for a procedural operation might list only the
request and reply:
B), and so
on. Splicing allows arbitrarily complex subprotocols to be inserted
between specified end-points. For example, a coarse-grained
specification of a rule for a procedural operation might list only the
request and reply:
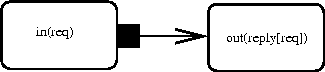
A refinement may then specify internal structure such as
an interaction with a helper:
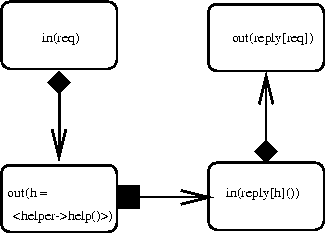
Note that even though the  was juggled around, the original
sense of the relation is maintained. If necessary, this may be checked
formally. For example here, the refined rule is of form (A
was juggled around, the original
sense of the relation is maintained. If necessary, this may be checked
formally. For example here, the refined rule is of form (A
 B)
B)  (B
(B  C)
C)  (C
(C  D). From the first two clauses we see that
A
D). From the first two clauses we see that
A  C. Then applying the last clause, we obtain A
C. Then applying the last clause, we obtain A
 D, as required by the original rule.
D, as required by the original rule.
A situation may be split into subsituations, so long as all ordering
relations are maintained across all paths along all subsituations.
For example, an initial rule for a boolean operation might say:
{in(req)} enable {out(reply(b))}
A refinement may split apart the conditions under which it replies
true versus false:
{in(req)} && {
case {badstuff()} enable {out(reply(FALSE))}
case {default} enable {out(reply(TRUE))}
}
The relation A  B or A
B or A  B may be strengthened
to A
B may be strengthened
to A  B when this does not conflict with other existing
rules. For example, a preliminary version of a rule may use
B when this does not conflict with other existing
rules. For example, a preliminary version of a rule may use  to indicate that a particular exception may result from a certain
request in a certain condition. Assuming that no other existing rules
indicate otherwise, a refinement may instead use
to indicate that a particular exception may result from a certain
request in a certain condition. Assuming that no other existing rules
indicate otherwise, a refinement may instead use 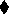 to make
the stronger claim that this exception is always generated under
this condition.
to make
the stronger claim that this exception is always generated under
this condition.
Similarly, we could strengthen the previous example to use the
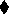 operator instead of
operator instead of  if we were sure that the
listed situations represented the only ways in which the TRUE
and FALSE replies could occur.
if we were sure that the
listed situations represented the only ways in which the TRUE
and FALSE replies could occur.
If relation A  B holds in an original
specification, a refinement may add a new rule A'
B holds in an original
specification, a refinement may add a new rule A'  B', where A
B', where A 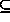 A' and B'
A' and B' 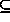 B. The reverse relation holds for
B. The reverse relation holds for  . These are situational
analogs of type conformance [59], ensuring that rules
applying in the original versions continue to hold even when refined.
For example, consider an A
. These are situational
analogs of type conformance [59], ensuring that rules
applying in the original versions continue to hold even when refined.
For example, consider an A  B rule for a
Relay r with attribute broken:
B rule for a
Relay r with attribute broken:
{in(m1), !broken(r)} lead {out(m2)}
In a refined version A'  B', we
could have a weaker left-hand-side (A
B', we
could have a weaker left-hand-side (A 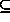 A') and
a stronger right-hand-side (B'
A') and
a stronger right-hand-side (B' 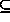 B), thus
logically subsuming the original version:
B), thus
logically subsuming the original version:
{in(m1)} lead {out(m2) by(r)}
The opposite maneuver would be either superfluous or an error: If the
second rule had been the original specification, then it would have
already covered the first rule. And if we had wanted to restrict
the second rule to the first, the relation would not be a refinement;
we would create an unrelated (on this dimension) protocol and/or
interface.
PSL constructs are based on structures describing possible worlds, as
found in model theory and temporal and modal
logic [32,20,66]. These serve as the basis for
several frameworks for specifying possibly distributed systems
[39,42,15,35,6], as well as related applied
temporal reasoning systems in AI and object-oriented logic programming
[44,3,17].
Possible world structures are of the form < W, V,
R>. W is a set of worlds. V is a set of value
expressions over some basis, with an associated function 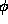 (p, w), which is true if expression p holds in world w.
R represents any number of defined relations among the worlds in
W. Chief among them is the relation generated by constraints.
PSL
(p, w), which is true if expression p holds in world w.
R represents any number of defined relations among the worlds in
W. Chief among them is the relation generated by constraints.
PSL  rules define the set of all worlds that are possible, and
a corresponding relation containing every pair of possible worlds.
rules define the set of all worlds that are possible, and
a corresponding relation containing every pair of possible worlds.
PSL situations define a another family of ``static'' equivalence
relations R . Situation S describes that set of
worlds for which its defining predicate P
. Situation S describes that set of
worlds for which its defining predicate P holds given the
values in the world (i.e.,
holds given the
values in the world (i.e., { w 
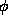 (P
(P  , w)
, w) }). In PSL this is expressed in terms of the matching relation,
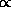 , between values holding in worlds and situation predicates.
The corresponding relation R
, between values holding in worlds and situation predicates.
The corresponding relation R contains all pairs of worlds
that are members of this set.
contains all pairs of worlds
that are members of this set.
The relation R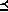 serves as the basis for PSL ordering
operators. This relation is simplest to describe formally when
expressions are restricted to event predicates on fixed
messages [24,70,58]. In this case, expressions in
V are just characteristic predicates of sets of event
occurrences, and
serves as the basis for PSL ordering
operators. This relation is simplest to describe formally when
expressions are restricted to event predicates on fixed
messages [24,70,58]. In this case, expressions in
V are just characteristic predicates of sets of event
occurrences, and 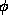 (e,w) is true if w contains the
events of e. For example, suppose a satisfies
e
(e,w) is true if w contains the
events of e. For example, suppose a satisfies
e = out(m1) for some message m1, and b
satisfies e
= out(m1) for some message m1, and b
satisfies e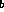 = out(m1) && in(m1). The relation
a
= out(m1) && in(m1). The relation
a 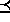 b states that e
b states that e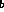
 e
e . The out(m1) event has not ``gone away'' in
B. In fact, if a
. The out(m1) event has not ``gone away'' in
B. In fact, if a 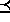 b, out(m1) holds no
later than the realization in which in(m1) holds as well. Thus,
when restricted to events, the relation R
b, out(m1) holds no
later than the realization in which in(m1) holds as well. Thus,
when restricted to events, the relation R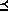 contains all
(a,b) such that the set of events described by e
contains all
(a,b) such that the set of events described by e must be be a subset of that described by e
must be be a subset of that described by e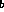 . When
expressions are liberalized to allow reference to arbitrary
attributes, the
. When
expressions are liberalized to allow reference to arbitrary
attributes, the 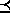 relation is no longer definable in this
semi-automatic manner, since it is not necessarily the case that
e
relation is no longer definable in this
semi-automatic manner, since it is not necessarily the case that
e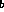
 e
e . Constraint rules must be
supplied to describe how arbitrary attributes vary with respect to
events.
. Constraint rules must be
supplied to describe how arbitrary attributes vary with respect to
events.



Next: Examples
Up: PSL: Protocols and Pragmatics
Previous: Specification
Doug Lea@Sat Jun 3 07:20:05 EDT 1995
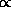 S for realization r and
situation S, holds if the situation predicate for S can be
made true using the values in r (see Appendix). Two or more
realizations may all match the same situation but in different ways
because they differently instantiate free parameters listed in the
situation.
S for realization r and
situation S, holds if the situation predicate for S can be
made true using the values in r (see Appendix). Two or more
realizations may all match the same situation but in different ways
because they differently instantiate free parameters listed in the
situation.

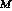 that minimally includes fields describing the message
``selector'' (e.g., operation name) and arguments (if any). We will
illustrate PSL usage in systems of fixed message types. However, at an
extreme, all messages in a system might have the same selector, with
an argument format requiring dynamic interpretation. Message types
may vary over any number of dimensions. For example, all messages of
a certain type may include fields suitable for use in routing over a
particular topology of distributed components.
that minimally includes fields describing the message
``selector'' (e.g., operation name) and arguments (if any). We will
illustrate PSL usage in systems of fixed message types. However, at an
extreme, all messages in a system might have the same selector, with
an argument format requiring dynamic interpretation. Message types
may vary over any number of dimensions. For example, all messages of
a certain type may include fields suitable for use in routing over a
particular topology of distributed components.
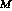 and p is a handle value, denotes a context in
which a particular message instance m has been received by
participant p, and out( m ) by( p )
denotes a context in which m has been issued by p. The
by( p ) suffixes are optional and seldom needed. When
otherwise unconstrained by context, omission reflects lack of
commitment about which participant issues or receives a message.
and p is a handle value, denotes a context in
which a particular message instance m has been received by
participant p, and out( m ) by( p )
denotes a context in which m has been issued by p. The
by( p ) suffixes are optional and seldom needed. When
otherwise unconstrained by context, omission reflects lack of
commitment about which participant issues or receives a message.
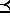 b
among two realizations a and a. If a
b
among two realizations a and a. If a 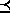 b, then a happens no later than a. (See Section
b, then a happens no later than a. (See Section

 B is akin to that of
a state transition, applying to cases in which As always precede
Bs. However, unlike a state transition, A
B is akin to that of
a state transition, applying to cases in which As always precede
Bs. However, unlike a state transition, A  B does not
indicate that instances of B form the ``next'' situations after
those of A. Instead, an instance occurs at some unspecified time
after an instance of A occurs, in a manner that neither requires nor
precludes concurrency or interleavings with respect to any other
non-conflicting rules. Also, unlike state transitions, the orderings
are not explicitly ``triggered'' by events. Instead predicates on
events are considered to be aspects of the situations themselves.
B does not
indicate that instances of B form the ``next'' situations after
those of A. Instead, an instance occurs at some unspecified time
after an instance of A occurs, in a manner that neither requires nor
precludes concurrency or interleavings with respect to any other
non-conflicting rules. Also, unlike state transitions, the orderings
are not explicitly ``triggered'' by events. Instead predicates on
events are considered to be aspects of the situations themselves.

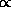 '') requires that unambiguous names be
used in any two situations related by operators. To ensure this, any
situation expression may reference, but not redeclare, any symbol
declared in its rules and its predecessors. Thus, all value
names in a set of ordered situations must be unique (see Appendix).
'') requires that unambiguous names be
used in any two situations related by operators. To ensure this, any
situation expression may reference, but not redeclare, any symbol
declared in its rules and its predecessors. Thus, all value
names in a set of ordered situations must be unique (see Appendix).

 B is used for relations in which A enables
B, applying to cases in which Bs are always preceded by
As. (Or are ``caused'' by As, under some interpretations
of this overloaded term.) For example, a desirable rule in most
systems is the no spurious replies rule, saying that replies are
sent only if messages are received. It does not say that requests
always lead to replies, only that replies are never sent unless
preceded by requests. In PSL/IDL, this rule is considered to be
predefined for all procedural requests, since it is enforced by CORBA:
B is used for relations in which A enables
B, applying to cases in which Bs are always preceded by
As. (Or are ``caused'' by As, under some interpretations
of this overloaded term.) For example, a desirable rule in most
systems is the no spurious replies rule, saying that replies are
sent only if messages are received. It does not say that requests
always lead to replies, only that replies are never sent unless
preceded by requests. In PSL/IDL, this rule is considered to be
predefined for all procedural requests, since it is enforced by CORBA:
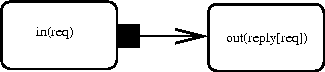
 'ed):
'ed):

 B operator is used
for if-and-only-if relations, in which both every A is followed
by a B, and every B is preceded by an A; thus
As and Bs occur only in pairs. For example, another desirable
global rule is the one-to-one delivery rule, for any m,
saying that all and only those messages that have been issued are
ultimately received.
B operator is used
for if-and-only-if relations, in which both every A is followed
by a B, and every B is preceded by an A; thus
As and Bs occur only in pairs. For example, another desirable
global rule is the one-to-one delivery rule, for any m,
saying that all and only those messages that have been issued are
ultimately received.

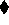 relation may be used to provide guarantees about
procedural operations. For example, we could strengthen the above
relation may be used to provide guarantees about
procedural operations. For example, we could strengthen the above
 form to assert that a reply to req must be issued,
thus precluding the possibility of exceptions or other non-procedural
behavior:
form to assert that a reply to req must be issued,
thus precluding the possibility of exceptions or other non-procedural
behavior:

 B
B  C. This indicates (A
C. This indicates (A  B)
B) 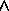 (B
(B
 C) while also extending scoping so that expressions in
C may reference terms in A. Chains across the other
operators are expressed similarly. For example, a special protocol in
which a relay outputs m3 after receiving the ordered fixed
messages m1 followed by m2 could include a rule of the
form:
C) while also extending scoping so that expressions in
C may reference terms in A. Chains across the other
operators are expressed similarly. For example, a special protocol in
which a relay outputs m3 after receiving the ordered fixed
messages m1 followed by m2 could include a rule of the
form:

 . The expression
. The expression  P indicates that P invariantly holds for all time, over all
possible worlds. All realizations must obey
P indicates that P invariantly holds for all time, over all
possible worlds. All realizations must obey  constraints in
addition to those explicitly listed in situations. In PSL/IDL
rules declarations, brace-demarcated expressions describing necessary
restrictions among attribute values are prefaced by inv. In
PSL/IDL-G, they are listed with an unfilled box on their sides. For
example:
constraints in
addition to those explicitly listed in situations. In PSL/IDL
rules declarations, brace-demarcated expressions describing necessary
restrictions among attribute values are prefaced by inv. In
PSL/IDL-G, they are listed with an unfilled box on their sides. For
example:

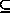 P.
P.
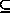 P, then fewer possible realizations match
Q than P. Every situation is a subsituation of the empty
situation
P, then fewer possible realizations match
Q than P. Every situation is a subsituation of the empty
situation 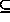
 B is expressed as
B is expressed as 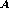
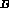
 B
as
B
as 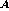
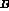

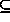 A. Strengthening may also occur by replacing a
predicate with one that implies it. For example, a situation
including out( m) might be strengthened by replacing it
with the more committal out( m)by( p ).
A. Strengthening may also occur by replacing a
predicate with one that implies it. For example, a situation
including out( m) might be strengthened by replacing it
with the more committal out( m)by( p ).
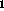 + S
+ S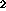 + ... + S
+ ... + S . This represents a set of
subsituations S
. This represents a set of
subsituations S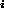 that are constrained to completely partition
a situation-space S. Partitioned subsituations must be
exhaustive and mutually exclusive. They cannot simultaneously
hold. Partitioning is thus one way to express the notion that one
situation ``disables'' another [
that are constrained to completely partition
a situation-space S. Partitioned subsituations must be
exhaustive and mutually exclusive. They cannot simultaneously
hold. Partitioning is thus one way to express the notion that one
situation ``disables'' another [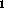
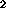 ...
... 

 B may be extended to A
B may be extended to A  S
S  B,
or to A
B,
or to A  B
B  S, or to the separate
(A
S, or to the separate
(A  S)
S) 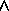 (A
(A  B), and so
on. Splicing allows arbitrarily complex subprotocols to be inserted
between specified end-points. For example, a coarse-grained
specification of a rule for a procedural operation might list only the
request and reply:
B), and so
on. Splicing allows arbitrarily complex subprotocols to be inserted
between specified end-points. For example, a coarse-grained
specification of a rule for a procedural operation might list only the
request and reply:

 was juggled around, the original
sense of the relation is maintained. If necessary, this may be checked
formally. For example here, the refined rule is of form (A
was juggled around, the original
sense of the relation is maintained. If necessary, this may be checked
formally. For example here, the refined rule is of form (A
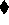 B)
B)  (B
(B  C)
C)  (C
(C 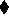 D). From the first two clauses we see that
A
D). From the first two clauses we see that
A  C. Then applying the last clause, we obtain A
C. Then applying the last clause, we obtain A
 D, as required by the original rule.
D, as required by the original rule.
 B or A
B or A  B may be strengthened
to A
B may be strengthened
to A 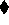 B when this does not conflict with other existing
rules. For example, a preliminary version of a rule may use
B when this does not conflict with other existing
rules. For example, a preliminary version of a rule may use  to indicate that a particular exception may result from a certain
request in a certain condition. Assuming that no other existing rules
indicate otherwise, a refinement may instead use
to indicate that a particular exception may result from a certain
request in a certain condition. Assuming that no other existing rules
indicate otherwise, a refinement may instead use 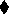 to make
the stronger claim that this exception is always generated under
this condition.
to make
the stronger claim that this exception is always generated under
this condition.
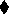 operator instead of
operator instead of  if we were sure that the
listed situations represented the only ways in which the TRUE
and FALSE replies could occur.
if we were sure that the
listed situations represented the only ways in which the TRUE
and FALSE replies could occur.
 B holds in an original
specification, a refinement may add a new rule A'
B holds in an original
specification, a refinement may add a new rule A'  B', where A
B', where A 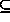 A' and B'
A' and B' 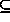 B. The reverse relation holds for
B. The reverse relation holds for  . These are situational
analogs of type conformance [
. These are situational
analogs of type conformance [ B rule for a
Relay r with attribute broken:
B rule for a
Relay r with attribute broken:
 B', we
could have a weaker left-hand-side (A
B', we
could have a weaker left-hand-side (A 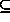 A') and
a stronger right-hand-side (B'
A') and
a stronger right-hand-side (B' 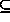 B), thus
logically subsuming the original version:
B), thus
logically subsuming the original version:
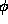 (p, w), which is true if expression p holds in world w.
R represents any number of defined relations among the worlds in
W. Chief among them is the relation generated by constraints.
PSL
(p, w), which is true if expression p holds in world w.
R represents any number of defined relations among the worlds in
W. Chief among them is the relation generated by constraints.
PSL  rules define the set of all worlds that are possible, and
a corresponding relation containing every pair of possible worlds.
rules define the set of all worlds that are possible, and
a corresponding relation containing every pair of possible worlds.
 . Situation S describes that set of
worlds for which its defining predicate P
. Situation S describes that set of
worlds for which its defining predicate P holds given the
values in the world (i.e.,
holds given the
values in the world (i.e., 
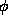 (P
(P  , w)
, w) 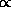 , between values holding in worlds and situation predicates.
The corresponding relation R
, between values holding in worlds and situation predicates.
The corresponding relation R contains all pairs of worlds
that are members of this set.
contains all pairs of worlds
that are members of this set.
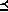 serves as the basis for PSL ordering
operators. This relation is simplest to describe formally when
expressions are restricted to event predicates on fixed
messages [
serves as the basis for PSL ordering
operators. This relation is simplest to describe formally when
expressions are restricted to event predicates on fixed
messages [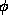 (e,w) is true if w contains the
events of e. For example, suppose a satisfies
e
(e,w) is true if w contains the
events of e. For example, suppose a satisfies
e = out(m1) for some message m1, and b
satisfies e
= out(m1) for some message m1, and b
satisfies e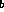 = out(m1) && in(m1). The relation
a
= out(m1) && in(m1). The relation
a 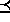 b states that e
b states that e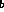
 e
e . The out(m1) event has not ``gone away'' in
B. In fact, if a
. The out(m1) event has not ``gone away'' in
B. In fact, if a 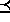 b, out(m1) holds no
later than the realization in which in(m1) holds as well. Thus,
when restricted to events, the relation R
b, out(m1) holds no
later than the realization in which in(m1) holds as well. Thus,
when restricted to events, the relation R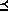 contains all
(a,b) such that the set of events described by e
contains all
(a,b) such that the set of events described by e must be be a subset of that described by e
must be be a subset of that described by e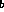 . When
expressions are liberalized to allow reference to arbitrary
attributes, the
. When
expressions are liberalized to allow reference to arbitrary
attributes, the 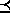 relation is no longer definable in this
semi-automatic manner, since it is not necessarily the case that
e
relation is no longer definable in this
semi-automatic manner, since it is not necessarily the case that
e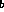
 e
e . Constraint rules must be
supplied to describe how arbitrary attributes vary with respect to
events.
. Constraint rules must be
supplied to describe how arbitrary attributes vary with respect to
events.